Rosche-Mervis 两氏*认为,概念在结构上编码有关成员该有的特性的统计式分析。所以一个原型意义上的概念意味着类里的一个典型成员。
比如对一些特性
| 性质 | 鸟类 | 杜鹃 | 鸡 | 秃鹫 |
|---|---|---|---|---|
| 有羽毛 | 是 | 是 | 是 | 是 |
| 会飞 | 是 | 是 | 否 | 是 |
| 会啼叫 | 是 | 是 | 否 | 否 |
| 会下蛋 | 是 | 是 | 是 | 是 |
| 体型小 | 是 | 是 | 否 | 否 |
| 树上筑巢 | 是 | 是 | 否 | 是 |
| 捕食昆虫 | 是 | 是 | 否 | 否 |
我们可以来做统计比较,即将某个东西用原型来比较。根据 Tversky, A. 的对比原则,相似度被定义为共同的性质减去差异
$$Sim(I,J)=a\times f(I\cap J)-b\times f(I-J)-c\times f(J-I)$$
其中 $a,b,c$ 是事先决定的权重,在这里我们令 $a=b=c=1$,那么
$$Sim(鸟类,杜鹃)=7-0-0=7$$
$$Sim(鸟类,鸡)=2-5-0=-3$$
所以<杜鹃>比起<鸡>是更典型的<鸟类>。这种判断也被称为「典型性效应」。Rosche 氏还发现了人们判断<苹果>比起<无花果>或者<橄榄>是更典型的<水果>,<萝卜>比起<洋葱>或者<黄瓜>是更典型的<蔬菜>。
概念的经典理论中,用来定义的所有性质都是必要的。但在原型论中不是,比如<鸡>是<鸟类>但并不拥有被认为属于<鸟类>的性质,比如<会飞><会啼叫><体型小><树上筑巢>。并且经典理论中诸性质的必要性在量上是相等的,而原型论中有权重变化。
一些论者**提出一些包括两种立场的理论,比如认为概念
具有经典理论的概念核心。这解释了概念如何进行合成和对概念进行本质判断
具有原型论的识别过程。这解释了误差和例外情形
原型在认知科学家们看来在心智中的对应表征有可能是,
一种假设中的「模范(=Exemplars)」,即被储存的一款例子,而非储存的诸例子的平均。
Lakoff 氏***主张原型可以被一些部分重叠的理想认知模型实现,而不必有真正的标准原型。
* Rosche, Mervis. Family Resemblances: studies in the internal structure of categories. Cog. Psy. 7 (1975).
** Osherson, Smith. On the adequacy of prototype theory as a theory of concepts. Cognition 9 (1981). 又见 Smith, Medin. Categories and Concepts (1981). 又见 Pinker. How the Mind Works. p. 126-127.
*** Lakoff, G. Women, Fire, and Dangerous Things (1987).
那么原型是否真的存在,是否真的是心智中的表征,需要用实验来回答。数据*显示受试确实在有更接近原型的概念中表现得更好,比如当受试能更快验证
杜鹃(robin)是一款鸟类
而处理这个句子则慢一些
鸵鸟(ostrich)是一款鸟类
研究者们于是假设受试们快速且诉诸直觉的判断调用了原型。在 Smith-Medin 两氏**提出的「积累器模型」中,分析是这样进行的:
当每个性质被拿来跟原型比较检验时,系统添加了或正或负的值给用来当积累器的寄存器。
当超过临界值时,系统就会判断当前考察的这个概念足够接近原型。
所以,有更多相同性质的概念会更快抵达临界值,从而会有更短的反应时间。
* Rips, Shoben, Smith. Semantic distance and the verification of semantic relations. J. Verb. Learn. Verb. Behav. 12 (1973). 又见 Pinker. How the Mind Works. p. 126.
** Smith, Medin. Concepts and Categories (1981).
第二个实验测试了受试的抽象能力。考虑到人们有能力从观测对象中抽象出一个可以用来学习和认识的「统计平均」,Posner-Keele 两氏*做了这个实验:
- 阶段1:给受试们展示一些点状图案(可能是三角形,字母或者随机),要求受试们分类,即记住每一个图案的种类。注意,这些图案没有自然的分类,心理学家称这样的分类为「虚设(nominal)」或者「特设(ad hoc)」。例子如图,其中周围四个图案多是中央原型的扭曲版本,数字表示扭曲程度。受试在这个阶段看不到原型。
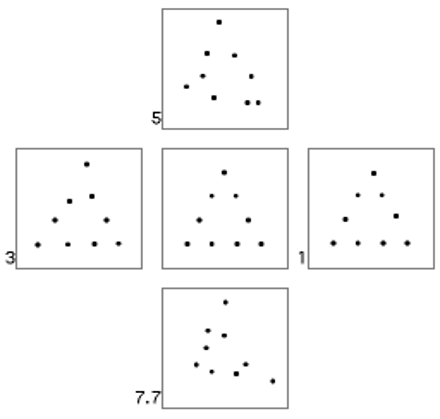
- 阶段2:给受试们的图案包括 (1) 先前的图案;(2) 先前的图案的平均也就是原型;(3) 新的图案,但是每个点都与原型图案的平均距离相同。
结果显示受试们最快分辨出先前图案和它们的原型。研究者们于是假设受试计算并且表征了先前图案及其平均,就像用统计过程抽象原型一样。
同样基于这个观察,Solso-McCarthy 两氏**关注的是人脸识别。他们的实验同样分为两个阶段
阶段1:给受试们展示一组脸的图片
阶段2:给受试们的图片包括 (1) 先前的脸;(2) 脸的平均或者说原型;(3) 新的脸。
结果是一样的,受试们更快识别出看过的脸及其原型。作为一个注记,深度学习算法有能力生成一些原型脸。
这种原型抽象能力还可以被一个简单的实验***呈现:受试们被展示一张教授办公室的照片,书架上刚好没有书。但是受试们经常错误地说书架本来是有书的。研究者推测受试可能诉诸了<教授办公室>的原型,而在这个原型中书架上典型地是有书的。这可能为虚假记忆(笔记#11)的现象做出了部分解释。
* Posner, Keele. On the Genesis of Abstract Ideas. J. Exp. Psy. 77 (1968).
** Solso, McCarthy. Prototype formation of faces: A case of pseudo-memory. British J. Psychology 72: 499-503.
*** Thagard, P. Mind (2005). p. 71.
原型论也有一些质疑。第一个方面,Armstrong 氏*观察到一个相当有趣的现象:受试们能够为经典概念<奇数><偶数>提供定义式结构,并且全数否认可以谈论这些成分性质的必要的程度,但仍然有典型性效应发生,即受试会认为「8比30更是典型的偶数」,「7比15更是典型的奇数」。这个典型性效应在速度和准确率方面也保持成立,受试处理更典型的概念更快(比如8比30更快),即便他们心里都有经典概念。所以典型性效应很可能不蕴含原型结构。那典型性效应蕴含的是什么?
可能是熟悉程度。人们用8的次数多过30,而无关概念的经典结构或者原型结构。
可能是证据推理。<会飞>是对<鸟类>更加可靠的提示。
另一方面,人们也拥有一些概念是没有对应的原型或者对平均成员的统计式信念的**。比如人们可能有<城市>的原型,或者<中国城市>的原型,但没法有<上海以南的沿海的中国城市>的原型。人们也没有对不存在实例的概念的原型,比如<31世纪最喜欢的纸片正太>。人们就是没有由高度不相似成员组成的类别的原型,比如<质量大于1g的物体>。人们同样没有逻辑概念的原型,比如<非猫>**和<若o则x>。
* Armstrong, Gleiman, Gleiman. What some concepts might not be (1983). 又见 Pinker. How the Mind Works. p. 127.
** Fodor. How the Mind Works. p. 101.